Thanks for inventing JavaScript · Widestring (indev)

'Thanks for inventing JavaScript' 밈 이미지. JavaScript의 특이한 코드 실행 결과 여러 개가 나열되어 있고, 그 밑에 JavaScript의 최초 개발자 브렌던 아이크의 웃는 얼굴과 함께 "Thanks for inventing Javascript"라는 문구가 있다.

어린 시절(나이가 1자리 수였을 때로 기억하고 있습니다)에 HTML 학습 사이트에 올라온 자바스크립트 달력 코드를 보고 따라해본 적이 있었습니다(실패했습니다). 또 나이가 더 들고 나서는 유명한 웹게임인 Cookie Clicker의 한국어 번역 플러그인을 만들다가 던진 기억이 있습니다.

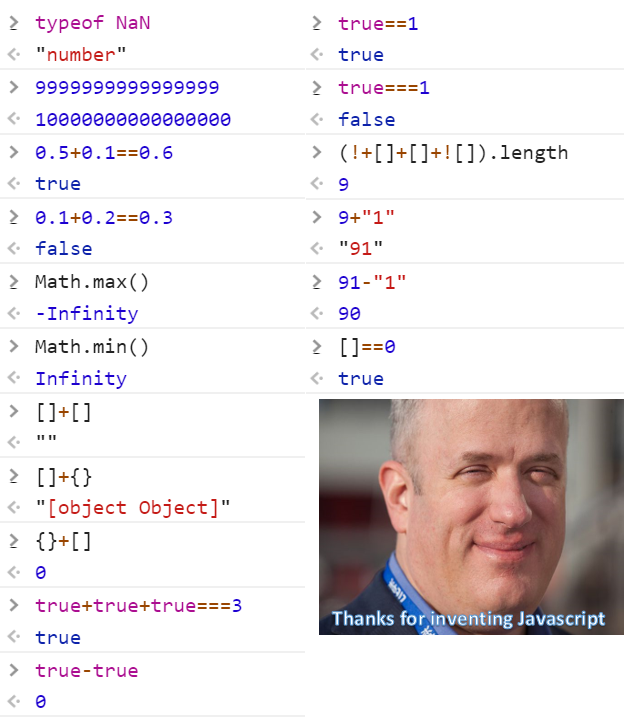
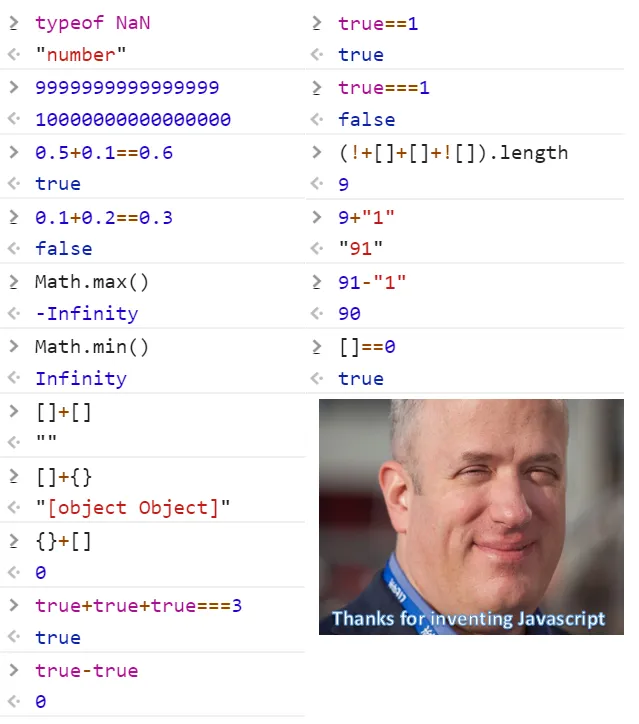
글 시작부터 좀 뜬금없는 얘기를 하긴 했는데, 아무튼 이런저런 이유로 자바스크립트가 마음의 고향인 저에게 이 "Thanks for inventing JavaScript" 짤을 보면 자바스크립트를 억지로 까고 있는 것 같아 신경쓰이는 점이 한두 가지가 아닙니다.

2022년에 이 신경쓰이는 점을 못 이겨 이 블로그 글을 처음 작성했고 2024년 1월 10일 당시 시크릿 모드로 Google에 thanks for inventing javascript을 검색한 결과에 첫 번째로 올라와 있었는데, 두 번째로 올라와 있는 이 글을 문득 읽어보니 제가 처음 썼던 글보다 훨씬 정성이 느껴져 부끄러웠습니다. 그런 의미로 원래보다 더 길고 자세하게 글을 재작성했는데, 더 깊이 있는 글이 되었으면 좋겠습니다.

이 글에서 언급하는 표준 문서는 [ECMA262]로, 독자의 편의를 위해 글쓴이가 임의로 번역했습니다. 해당 표준에서 정의해서 사용하는 내부 연산 및 표기도 그대로 옮겼지만, 글을 이해하는 데 필요한 것은 아니고 알고리즘의 전체적인 흐름만 이해하면 됩니다. 단, 아래 표기는 알아두는 것이 좋습니다.

청록색 기울임꼴로 된 텍스트는 그 알고리즘에서 사용하는 변수명입니다.
굵은 텍스트는 JavaScript 값입니다.
JavaScript의 Number 값은 아래 첨자 를 붙여 수학적 실수 값과 구분합니다.
연산 앞에 물음표(?)가 붙는 경우는 '그 연산이 (break, continue, return, throw 등에 의해) 비정상적으로 종료된 경우 즉시 반환한다'고 해석할 수 있습니다. 일종의 예외 처리인 것으로 생각할 수 있으며, 무시하고 읽어도 큰 문제는 없습니다.
- 비슷하게 연산 앞에 느낌표(!)가 붙는 경우는 '그 연산은 비정상적으로 종료되지 않는다'는 불변조건으로 해석할 수 있습니다. 역시 무시해도 됩니다.

참고로 구글 이미지검색을 해본 결과 이 이미지는 2018년 6월 21일에 레딧의 r/ProgrammerHumor에 처음 올라왔던 것으로 보입니다. 이 이전의 검색결과 중 실제로 해당 이미지가 있는 페이지는 찾지 못했습니다.

`typeof NaN`

어떻게 된 걸까?

typeof 연산자의 13.5.3.1 런타임 의미론: 평가^{Runtime Semantics: Evaluation}에서 typeof 연산자의 알고리즘을 확인할 수 있는데, 중요하게 볼 만한 부분만 간추리면 이렇습니다.

UnaryExpression : typeof UnaryExpression
val을 UnaryExpression의 ? 평가값으로 정한다.
(중략)
val이 Number일 경우, "number"를 반환한다.

UnaryExpression : typeof UnaryExpression
Let val be ? Evaluation of UnaryExpression.
...
If val is a Number, return "number".

그런데 6.1.6.1 Number 타입^{The Number Type}에서는 NaN도 Number인 것으로 정의하고 있습니다.¹

Number 타입은 정확히 18,437,736,874,454,810,627(즉, )개의 값을 가지고, 배정밀도 부동소수점의 IEEE 754-2019 binary64 값을 IEEE 이진 부동소수점 산술 표준에서 명시한 대로 나타내나, IEEE 표준의 9,007,199,254,740,990(즉, )개의 서로 다른 NaN 값은 ECMAScript에서 특수한 단일 NaN 값으로 나타내어진다. (NaN 값은 프로그램 표현식 NaN으로 생성됨에 유의하라.) ...

The Number type has exactly 18,437,736,874,454,810,627 (that is, ) values, representing the double-precision floating point IEEE 754-2019 binary64 values as specified in the IEEE Standard for Binary Floating-Point Arithmetic, except that the 9,007,199,254,740,990 (that is, ) distinct NaN values of the IEEE Standard are represented in ECMAScript as a single special NaN value. (Note that the NaN value is produced by the program expression NaN.) ...

무엇이 문제일까?

바로 위의 인용문에서 주목할 점이 있습니다.

... IEEE 표준의 9,007,199,254,740,990(즉, )개의 서로 다른 NaN 값은 ...

NaN 값은 애초에 IEEE 754 표준에서 정의하는 값이고, 절대 다수의 부동소수점 연산이 IEEE 754를 따르기 때문에 JavaScript에서도 포함하고 있습니다. 하필이면 이 값에 '수가 아니다'라는 의미의 이름이 붙었고 JavaScript가 기본 수 타입에 "number"라는 이름을 붙여버려서 혼란이 생겼다는 느낌이 들긴 합니다.

다른 언어에서도 그럴까?

네. NaN이 있는 다른 언어에서도 NaN은 다른 부동소수점 실수와 똑같은 타입을 가지고, JavaScript만 NaN을 다른 타입으로 취급한다면 오히려 이상할 것입니다.

#include <iostream>
#include <cmath>
#include <typeinfo>

template<class T> void print_type(T x) {
	std::cout << typeid(x).name() << " " << x << std::endl;
}

int main() {
    double
		number = 12.34,
		not_a_number = 0./0.,
		explicit_nan = NAN;

	/*
		`typeid(...).name()`은 컴파일러에 따라 다른 값을 반환할 수 있지만,
		같은 컴파일러에서 같은 타입이면 같은 문자열을 반환합니다.
	*/
	print_type(number); // d 12.34
	print_type(not_a_number); // d nan
	print_type(explicit_nan); // d nan
    return 0;
}

from math import nan

def print_type(x):
	print(type(x), x)

print_type(1.) # <class 'float'> 1.0
# Python에서는 0으로 나누면 NaN을 반환하는 대신 ZeroDivisionError가 발생합니다.
# print_type(0./0.)
print_type(nan) # <class 'float'> nan

`9999 9999 9999 9999`

이 단락을 포함해 길이가 긴 수를 작성할 때는 독자의 편의를 위해 네 자리마다 띄어쓰기로 자릿수를 구분합니다.

어떻게 된 걸까?

이것도 IEEE 754 문제입니다.

9999 9999 9999 9999를 이진법으로 쓰면 10 0011 1000 0110 1111 0010 0110 1111 1100 0000 1111 1111 1111 1111이고 맨 앞의 1을 제외하면 가수^significand^역1가 53자리인데, 배정밀도 부동소수점은 가수가 52자리밖에 없어 이 값을 표현할 수 없습니다. 그 대신 가장 가까운 표현 가능한 값으로 반올림한 결과가 1 0000 0000 0000 0000입니다.

아니면 float.exposed에 부동소수점 값을 입력하면 그 값의 내부 표현을 볼 수 있는데, 9999 9999 9999 9999의 경우 1 0000 0000 0000 0000.0으로 반올림되고, 그 부호-지표-가수 값이 다음과 같습니다.

부호^sign = 0
- 0이면 양수, 1이면 음수입니다.
지표^exponent = 1076
- 이 값에서 1023을 뺀 값이 소수점의 위치가 됩니다. 이므로 소수점이 (이진법 표현에서) 왼쪽으로 53자리 이동합니다.
가수^significand = 496 4003 7262 9504
- 이 값은 이진법으로 0001 1100 0011 0111 1001 0011 0111 1110 0000 1000 0000 0000 0000인데(위에서 언급했듯이 52자리입니다), 이 앞에 1.을 붙인 1.0001 1100 0011 0111 1001 0011 0111 1110 0000 1000 0000 0000 0000에서 소수점을 적절히 움직인 것이 실제 값이 됩니다.

여기서 가수를 1 내리면 아니나다를까 9999 9999 9999 9998.0이 됩니다.

다른 언어에서도 그럴까?

네.

#include <stdio.h>

int main(void) {
	double gazillion = 9999999999999999.;
    printf("%f\n", gazillion); // 10000000000000000.000000
    return 0;
}

해결할 수 있을까?

진짜로 정수 9999 9999 9999 9999를 정확히 표현하고 싶다면 BigInt 9999_9999_9999_9999n을 쓰면 됩니다². 단, 소수는 표현할 수 없으며 BigInt끼리만 연산할 수 있습니다.

`0.1+0.2==0.3`

어떻게 된 걸까?

이것도 IEEE 754 문제입니다.

역시 float.exposed(무관하지만 주소가 외우기 정말 좋네요)에 0.1, 0.2, 0.3, 0.3000 0000 0000 0000 4를 입력하면 이렇게 됩니다.

0.1 → 0.1000 0000 0000 0000 0555 1
- 부호 = 0
- 지표 = 1019
- 가수 = 2702 1597 7642 2298 (십진법), 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 (이진법)
0.2 → 0.2000 0000 0000 0000 1110 2
- 부호 = 0
- 지표 = 1020
- 가수 = 2702 1597 7642 2298 (십진법), 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 (이진법)
0.3 → 0.2999 9999 9999 9999 8889 8
- 부호 = 0
- 지표 = 1021
- 가수 = 900 7199 2547 4099 (십진법), 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 (이진법)
0.3000 0000 0000 0000 4 → 0.3000 0000 0000 0000 4440 9
- 부호 = 0
- 지표 = 1021
- 가수 = 900 7199 2547 4100 (십진법), 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0100 (이진법)
  - 바로 위의 0.3보다 가수만 1 큽니다.

0.1 0.2 0.3 모두 이진법으로 표현하면 순환소수가 되기 때문에 가장 가까운 부동소수점으로 반올림이 되는데, 이때 생긴 오류가 누적되면서 생기는 현상입니다.

바로 위 줄에서는 0.5+0.1==0.6이 성립하는데, 이는 0.5가 배정밀도 부동소수점으로 정확히 표현 가능하기 때문입니다.

0.5
- 부호 = 0
- 지표 = 1022
- 가수 = 0 (십진법), 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 (이진법)

다른 언어에서도 그럴까?

게임메이커 언어에도 이 문제가 있어서 블로그에서 언급한 적이 있습니다. 심지어 유명한 프로그래밍 언어에서 0.1 + 0.2를 한 결과를 모은 웹페이지도 있습니다.

`Math.max()`

어떻게 된 걸까?

21.3.2.25 Math.max(...args)에서 이 함수의 알고리즘을 확인할 수 있습니다.

coerced를 새로운 비어 있는 리스트로 정한다.

args의 각 원소 arg마다,
n을 ? ToNumber(arg)로 정한다.
coerced의 맨 끝에 n을 추가한다.

highest를 로 정한다.

coerced의 각 원소 number마다,
number가 NaN이면, NaN을 반환한다.
number가 이고 highest가 이면, highest를 로 바꾼다.
number > highest이면, highest를 number로 바꾼다.

highest를 반환한다.

Let coerced be a new empty List.

For each element arg of args,
Let n be ? ToNumber(arg).
Append n to coerced.

Let highest be .

For each element number of coerced,
If number is NaN, return NaN.
If number is and highest is , set highest to .
If number > highest, set highest to number.

Return highest.

이때 args가 빈 배열이면 coerced도 빈 리스트가 되고, 4번 단계가 실행되지 않기 때문에 highest의 초깃값인 , 즉 -Infinity를 반환합니다.

21.3.2.26 Math.min(...args)도 무한대의 부호와 부등호의 방향을 제외하면 같은 알고리즘을 사용합니다.

무엇이 문제일까?

Math.max는 애초에 인자로 주어진 수 중에 가장 큰 수를 구하는 함수지, 무턱대고 가장 큰 수를 반환하는 함수가 아닙니다. -Infinity가 아니라 Infinity일 이유가 전혀 없습니다.

인자를 0개 전달받았을 때 그냥 throw를 해도 되긴 하지만, -Infinity를 반환하겠다면 그 이유를 수학적으로 정당화할 수 있습니다. (실수의) 덧셈에는 항등원, 즉 와 를 만족하는 이 있고, 모든 덧셈은 암묵적으로 항등원이 붙는 것으로 생각할 수 있습니다.

즉, "0개의 수를 더하는 것"은 "덧셈의 항등원에 0개의 수를 더하는 것", 즉 그냥 덧셈의 항등원이 되는 것으로 이해할 수 있습니다.

한편 연산에도 와 를 만족하는 항등원이 있는데, 이 값이 다름아닌 입니다.³ 즉, 위와 같은 논리로 0개의 수의 최댓값은 인 것으로 생각할 수 있습니다. 이 논리는 Math.min() == Infinity에도 똑같이 적용할 수 있습니다.⁴

해결할 수 있을까?

JavaScript에서 각 분야별로 가장 큰/작은 Number 타입의 수는 다음과 같이 구할 수 있습니다.

가장 큰/작은 수: Infinity/-Infinity
가장 큰 유한수: Number.MAX_VALUE = 1.7976 9313 4862 3157e+308
정확히 나타낼 수 있는 가장 큰/작은 정수: Number.MAX_SAFE_INTEGER = 9007 1992 5474 0991/Number.MIN_SAFE_INTEGER = -9007 1992 5474 0991
가장 작은 양수: Number.MIN_VALUE = 5e-324

`[]+[]`, `[]+{}`, `{}+[]`

(!+[]+[]+![]).length, 9+"1", 91-"1"은 생략하겠습니다.

어떻게 된 걸까?

덧셈 연산자의 의미는 13.15.4 EvaluateStringOrNumericBinaryExpression(leftOperand, opText, rightOperand)를 거쳐 13.15.3 ApplyStringOrNumericBinaryOperator(lVal, opText, rVal)에서 정의됩니다. 이 글에서 중요하게 볼 만한 부분만 간추리면 다음과 같으며, 이 경우에는 opText가 +입니다.

opText가 +일 경우,
lPrim을 ? ToPrimitive(lVal)로 정한다.
rPrim을 ? ToPrimitive(rVal)로 정한다.
lPrim이 String이거나 rPrim이 String일 경우,
lStr을 ? ToString(lPrim)으로 정한다.⁵
rStr을 ? ToString(rPrim)으로 정한다.
lStr와 rStr의 연결문자열을 반환한다.
(후략)

(후략)

If opText is +,
Let lPrim be ? ToPrimitive(lVal).
Let rPrim be ? ToPrimitive(rVal).
If lPrim is a String or rPrim is a String,
Let lStr be ? ToString(lPrim).
Let rStr be ? ToString(rPrim).
Return the string-concatenation of lStr and rStr.
...

...

여기서 7.1.1 ToPrimitive(input[, preferredType])는 Object인 값을 Object가 아닌 원시값으로 바꾸는 연산이며, []와 {}의 경우에는 모두 .toString()을 호출하는 연산이 됩니다.

[]+[]와 []+{}은 모두 이항 덧셈 연산자의 의미로 설명할 수 있습니다.

[].toString() = ""이므로 []+[] = "" + "" = ""입니다.
{}.toString() = "[object Object]"이므로 []+{} = "" + "[object Object]" = "[object Object]"가 됩니다.

다만, {}+[]는 예외적으로 객체 {}와 배열 []을 더하는 것이 아니라 비어 있는 블록 {}과 배열에 단항 덧셈을 하는 표현식 +[]으로 파싱되기 때문에 다른 결과가 나옵니다. 이 값은 ToNumber(argument = []), ToPrimitive(input = [], preferredType = NUMBER)를 거쳐 ""이 된 뒤 ToNumber(argument = ""), StringToNumber(str = ""), 마지막으로 StringNumericValue(StringNumericLiteral ::: StrWhiteSpace_opt)의 많은 단계를 거쳐 , 즉 0이 됩니다. +[] = 0이라는 내용을 이렇게까지 늘여서 써도 되나...? 참고로 ({}+[])은 정상적(?)으로 "[object Object]"가 됩니다.

무엇이 문제일까?

어... 이건(특히 처음 두 개는) 언어 설계의 잘못이라는 게 개인적인 의견입니다. 혹시 (!+[]+[]+![]).length에 흥미가 생기신다면 이 페이지도 확인해 보세요.

`true+true+true===3`, `true-true`

어떻게 된 걸까?

덧셈 연산자의 평가 알고리즘을 다시 한 번 살펴봅시다. 이 경우에도 opText가 +입니다.

opText가 +일 경우,
lPrim을 ? ToPrimitive(lVal)로 정한다.
rPrim을 ? ToPrimitive(rVal)로 정한다.
(중략)
lVal을 lPrim으로 바꾼다.
rVal을 rPrim으로 바꾼다.

참고: 이 시점에 이 연산은 수 연산으로 확정된다.

lNum을 ? ToNumeric(lVal)로 정한다.

rNum을 ? ToNumeric(rVal)로 정한다.

(중략)

lNum이 BigInt일 경우,
(중략)

그렇지 않을 경우,
불변조건: lNum은 Number이다.
operation을 아래 표에서 opText에 대응하는 추상 연산으로 정한다. (표 생략)

operation(lNum, rNum)을 반환한다.

If opText is +,
Let lPrim be ? ToPrimitive(lVal).
Let rPrim be ? ToPrimitive(rVal).
...
Set lVal to lPrim.
Set rVal to rPrim.

NOTE: At this point. it must be a numeric operation.

Let lNum be ? ToNumeric(lVal).

Let rNum be ? ToNumeric(rVal).

...

If lNum is a BigInt, then
...

Else,
Assert: lNum is a Number.
Let operation be the abstract operation associated with opText in the following table: ...

Return operation(lNum, rNum).

이때 ToNumeric(value = true)는 ToPrimitive(input = true, preferredType = NUMBER)와 ToNumber(argument = true)를 거쳐 , 즉 1이 됩니다. 또한 7번째 단계에서 언급한 표를 옮기지는 않겠지만 opText = +에 대응하는 연산은 Number::add이고, 이 연산은 보통의 덧셈 연산이므로 결과적으로는 이 됩니다. true-true도 비슷한 과정을 거쳐 이 됩니다.

무엇이 문제일까?

제 개인 의견을 말씀드리자면, true에 1을, false에 0을 대응시키는 것은 매우 자연스러운 현상이고, JavaScript의 잘못이 있다면 위의 []+[]이나 []+{}처럼 부울을 정수로 암시적으로 형변환한 것 정도입니다. 최소한 []을 ""으로, {}를 "[object Object]"로 변환한 것보다는 직관적이지 않나요?

다른 언어에서도 그럴까?

적어도 C++와 Python에도 부울을 정수로 암시적으로 형변환하는 동작이 있습니다.

#include <iostream>
#include <typeinfo>

template<class T> void print_type(T x) {
	std::cout << typeid(x).name() << " " << x << std::endl;
}

int main() {
	print_type(true); // b 1
	print_type(true + true + true); // i 3
	print_type(true - true); // i 0
    return 0;
}

def print_type(x):
	print(f"{type(x)} {x}")

print_type(True) # <class 'bool'> True
print_type(True + True + True) # <class 'int'> 3
print_type(True - True) # <class 'int'> 0

`true==1`, `true===1`, `[]==0`

어떻게 된 걸까?

== 연산자의 의미는 7.2.13 IsLooselyEqual(x, y), === 연산자의 의미는 7.2.14 IsStrictlyEqual(x, y)에서 정의하고 있는데, 이유는 잘 모르겠지만 연산자의 좌변과 우변이 추상 연산에서는 바뀌어서 호출되고 있습니다. 표준에 'A == B와 B == A는 A와 B의 연산 순서를 제외하면 동등하다'는 언급이 있으므로 큰 문제는 없습니다.

IsStrictlyEqual(x, y)는 두 값의 타입까지 일치해야 하는 동일성 비교 연산입니다.

SameType(x, y)가 false일 경우, false를 반환한다.

(후략)

If SameType(x, y) is false, return false.

...

IsLooselyEqual(x, y)는 두 값의 타입이 다를 때 형변환을 해서 비교하는 연산입니다.

SameType(x, y)가 true일 경우,
IsStrictlyEqual(x, y)를 반환한다.
(중략)
x가 Number이고 y가 String일 경우, ! IsLooselyEqual(x, ! ToNumber(y))를 반환한다.
(중략)
y가 Boolean일 경우, ! IsLooselyEqual(x, ! ToNumber(y))를 반환한다.
x가 String, Number, BigInt, Symbol 중 하나이고 y가 Object일 경우, ! IsLooselyEqual(x, ! ToPrimitive(y))를 반환한다.
(후략)

If SameType(x, y) is true,
Return IsStrictlyEqual(x, y).
...
If x is a Number and y is a String, return ! IsLooselyEqual(x, ! ToNumber(y)).
...
If y is a Boolean, return ! IsLooselyEqual(x, ! ToNumber(y)).
If x is either a String, a Number, a BigInt, or a Symbol and y is an Object, return ! IsLooselyEqual(x, ! ToPrimitive(y)).
...

위의 세 비교 연산은 다음 순서대로 진행됩니다.

true==1 (x = , y = true)
1. y가 Boolean이므로 y를 ToNumber(y) = 로 바꾸고 다시 비교합니다. (x = , y = )
2. x와 y가 같은 타입이므로 IsStrictlyEqual로 비교합니다.
3. x와 y가 NaN이 아니고 같은 값을 가지므로 true를 반환합니다.
true===1 (x = , y = true)
1. x와 y가 다른 타입이므로 false를 반환합니다.
[]==0 (x = , y = [])
1. x가 Number이고 y가 Object이므로 y를 ToPrimitive(y) = ""로 바꾸고 다시 비교합니다. (x = , y = "")
2. x가 Number이고 y가 String이므로 y를 ToNumber(y) = 로 바꾸고 다시 비교합니다. (x = , y = )
3. x와 y가 같은 타입이므로 IsStrictlyEqual로 비교합니다.
4. x와 y가 NaN이 아니고 같은 값을 가지므로 true를 반환합니다.

무엇이 문제일까?

이것도 []+[]처럼 JavaScript 잘못이 맞아서 제가 뭐라고 할 수가 없긴 한데, 대신 2021년 8월에 봤던 이 글(영어)을 공유해드릴 수는 있을 것 같습니다.

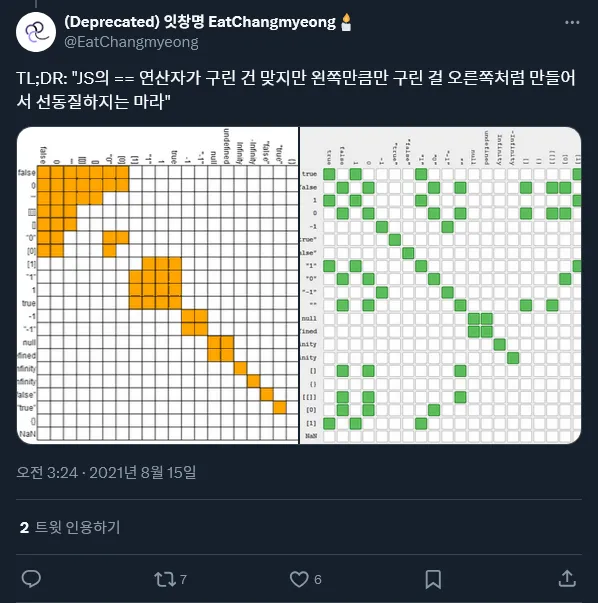
잇창명의 2021년 8월 15일 X 게시물: "TL;DR: "JS의 == 연산자가 구린 건 맞지만 왼쪽만큼만 구린 걸 오른쪽처럼 만들어서 선동질하지는 마라"". 위에 링크된 글에서 게시한 주황색 표와 초록색 표가 이미지로 첨부되어 있다.

결론

JavaScript의 문제가 아닌 걸 치우고 IEEE 754의 문제만 따로 모아놓으면 이 정도가 됩니다.

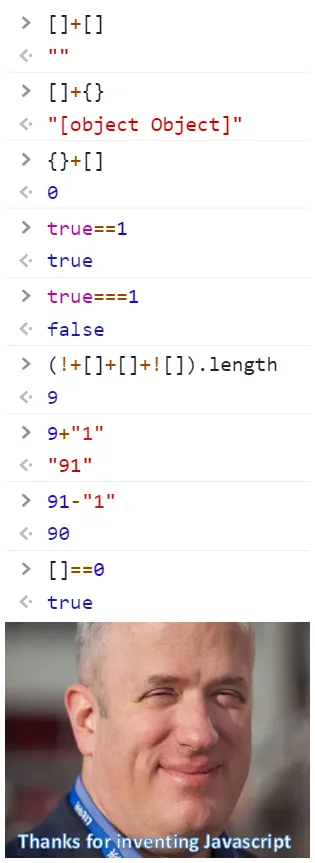
위의 "Thanks for inventing Javascript" 이미지에서 자바스크립트 자체의 문제인 코드만 남겼다.

위의 "Thanks for inventing Javascript" 이미지에서 IEEE 754의 문제인 코드만 남기고 문구를 "Thanks for inventing IEEE 754"로 수정했다.

차라리 JavaScript를 이렇게 깠으면 저도 ~~트위터에~~ X에 블루스카이에 "자바스크립트넘구데기" 같은 자조적인 글을 쓰면서 저 짤을 올렸을 겁니다. 맨 위의 짤은 JavaScript 자체의 문제가 아닌 것을 슬쩍 끼워넣어서 문제의 본질을 흐리고 있습니다. 애초에 그냥 웃자고 만든 밈짤인데 민감하게 반응한 감도 없지는 않지만, 누군가는 이 얘기를 해야 한다고 항상 생각하고 있었습니다. 아무튼 저는 할 말을 전부 했으니 여한이 없습니다. 😝

각주

¹ ECMA-262 표준에서 정의하는 "언어 타입^{language types}"은 typeof가 반환하는, '사용자에게 노출되는' 타입과 다소 차이가 있는데, null은 Object가 아닌 별도의 Null 타입으로, typeof가 "function"인 값은 내부 메소드 [[Call]]이 있는 Object 타입으로 분류되어 있습니다. ↑

² ES2021부터 수를 작성할 때는 숫자 사이에 _ 문자를 삽입해서 자릿수를 구분할 수 있으며, 소수점 앞뒤, 지수 자리, 이진수, 팔진수, 십육진수, BigInt를 모두 지원합니다. ↑

³ 엄밀히 말해 max의 항등원은 확장된 실수, 즉 ±∞가 추가된 실수 체계에서만 정의되며, 일반적인 실수 집합에서는 max의 항등원이 존재하지 않습니다. 추가로 JavaScript의 Number에는 NaN이 정의되어 있는데, max(NaN, -∞) = max(-∞, NaN) = NaN이므로 문제가 없습니다. ↑

⁴ 물론 더 엄밀하게 따지면 최댓값과 최솟값은 주어진 집합의 원소 중에서 골라야 하는 값이므로 공집합에 대해서 정의되지 않기 때문에, 이렇게 정의할 거면 이름을 supremum/infimum으로 지어야 한다는 반박이 가능합니다. ↑

⁵ ToString은 String이 아닌 값을 String인 값으로 바꾸는 추상 연산입니다. 이 맥락에서는 lPrim과 rPrim이 모두 String이므로 의미 있는 동작을 하지 않습니다. ↑

역주

^역1 상용로그의 지표와 가수 개념에서 번역어를 차용했습니다. ↑

참고 문헌

^[ECMA262] ECMA-262 ECMAScript® 2026 Language Specification. 2025년 8월 21일 현재 2026년판으로, 판올림 시 목차 번호나 세부 알고리즘이 바뀔 수 있지만 글의 취지에는 영향이 없습니다. ↑

typeof NaN

어떻게 된 걸까?

무엇이 문제일까?

다른 언어에서도 그럴까?

9999 9999 9999 9999

어떻게 된 걸까?

다른 언어에서도 그럴까?

해결할 수 있을까?

0.1+0.2==0.3

어떻게 된 걸까?

다른 언어에서도 그럴까?

Math.max()

어떻게 된 걸까?

무엇이 문제일까?

해결할 수 있을까?

[]+[], []+{}, {}+[]

어떻게 된 걸까?

무엇이 문제일까?

true+true+true===3, true-true

어떻게 된 걸까?

무엇이 문제일까?

다른 언어에서도 그럴까?

true==1, true===1, []==0

어떻게 된 걸까?

무엇이 문제일까?

결론

`typeof NaN`

`9999 9999 9999 9999`

`0.1+0.2==0.3`

`Math.max()`

`[]+[]`, `[]+{}`, `{}+[]`

`true+true+true===3`, `true-true`

`true==1`, `true===1`, `[]==0`